Friday, 29 July 2011
Have you ever really played with Legos? I’m talking about a full-sensory experience; an immersion into the world of humanity’s greatest building materials. I know, it’s a tough question to answer. Allow me to show you what I mean, using my beautiful assistant as a model—
First, get into the bin of Legos:
Next, ensure that you’re comfortable. If your tongue is hanging out, that’s a good sign.
Then, just stretch out and enjoy the full-body comfort of sitting on a bed of Legos:
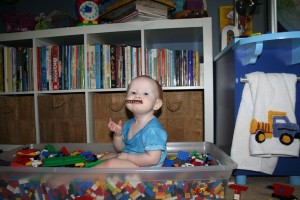
Dig:
And play:
And don’t let the fact that you only have six teeth stop you from eating these tasty bits of plastic. Legos…yum!
Finally, if some bigger, smarter, ‘parental’ adult tries to take you out of the bin for fear that you’re gonna choke on a brick, you sass off to them as if you freakin’ own these Legos.
Saturday, 30 July 2011
This evening, my son and I watched the Star Trek episode “The Terratin Incident.” The main plot of the episode features the crew shrinking in size and unsure how to correct the problem.
Why they are shrinking and how the solve the matter is not important here (though you can click the link above and spoil the crap out of the story for yourself, if you wish). What I will divulge, however, is that the crew initially are unsure if they are shrinking or if the ship, and everything in the ship, are enlarging. Their clothes, incidentally, are shrinking right along with them (since they’re also made of organic material), but their jewelery stays the same size; Nurse Chapel remarks that her arm band could now be used as a necklace.
There are a number of gaffes and missed opportunities in this episode, but the first one to strike me was this: How in the galaxy could the crew not realize that they are shrinking? I mean, think about it, if you wake up tomorrow and everything in your home is double the size it was the night before, would you wonder if your bed, walls, blankets, clocks, and everything else expanded? Or would you, rather, conclude that you had shrunk?
This whole scenario reminded me of a(n) (ex-)friend who used to raise all sorts of obscure questions, mostly just for laughs. On a couple of occasions, he asked: If everything – everything – double in size right now, would we notice?
My immediate answer the first time he posed this inquiry was, “of course!” I replied by saying, “Wouldn’t it be obvious that the sun was twice as big in the sky?” But then my friend would show me the level of complexity in his subtly simple question by responding, “No, it wouldn’t be obvious because, remember, EVERYTHING would double in size – thus the distance between Earth and the sun would also have doubled, and therefore you wouldn’t notice the sun’s increased diameter.”
This would then open up a volley of inquiries and retorts, every time my friend noting that I had forgot something.
But here’s the final answer: Yes, you would notice. I was right all along, I just failed at providing the reasons why. For one thing, doubling the distance between Earth and its star would create a noticeable drop off in gravitational pull – the earth’s rate of revolution would slow – a drop off that would not be counteracted by a doubling of the sun’s mass. Additionally, doubling the strength of gravity would be rather negligible compared to the doubling of the nuclear forces – atoms would have a tougher time forming molecules, and radioactivity would slow. More pedestrian, doubling the population of the city I live in would be immediately noticeable, even with a doubling of the city’s area.
In fact, I would add that my friend’s question does not even make sense, because it would be impossible for everything to double in size. As an example, let’s look at a very square place to live: Colorado.
Colorado has four sides: its north and south borders are approximately 378 miles long, and its east and west borders are approximately 276 miles long. This gives Colorado a land area of roughly 104,300 square miles.
Now, let’s do what my friend says and double the size of everything:
Now Colorado has north and south borders that are 756 miles long, and east and west borders that are 552 miles long. So far, so good, right? Except that now, Colorado’s land area is about 417,300 square miles – quadruple what it was before. Uh-oh.
Anyway, if you’re reading this Andy: Thanks for the great mental exercises.











If CO were square, wouldn’t it have to be the same length on all 4 sides?
I only said it was “very square,” meaning that it is rather close to a true square compared with other states (except maybe Wyoming).
I think that if I were to take one of the 2×2 LEGO bricks and try the doubling exercise, I might be tempted to put another 2×2 brick next to it and then another one above it and then one more kitty corner from the original. Then I’d make sure I did my doubling correctly by counting the pips across one direction (1,2,3,4) and then in the other direction (1,2,3,4) and that would satisfy the length and width doubling. Then I’d count the total number of pips and see that I’ve gone from four pips to sixteen — Uh oh.
But then I’d realize that I didn’t double the size of the pips and I didn’t double the distance between the pips. I didn’t really double EVERYTHING — Uh oh.
So then I’d get a LEGO DUPLO brick and try again. A LEGO DUPLO is double the width and double the length of a LEGO brick (also double the height). What’s more, the pips are double in size and are spaced at double the distance apart from the pips on a LEGO brick.
So now let’s count. Number of pips in this direction? One, Two. In this direction? One, Two. Total number of pips? One, Two, Three, Four. Ratios preserved.
Or in the case of Colorado, double the size of the ruler.
I see what you’re saying, and this is the kind of discussion I used to have with my friend on this topic.
The problem he and I would have with doubling is that it’s impossible to know where to stop. A DUPLO is twice as long, high, and wide as its LEGO counterpart. This doubled version would probably be impossible to distinguish from its original size. I could imagine taking a picture of a LEGO, then taking a picture of its DUPLO counterpart and, if the camera was set up correctly, it WOULD be impossible to tell them apart. I could even set up a bogus ruler next to the DUPLO to give the impression that it’s the same thing as the LEGO. However, we’ve kind of cheated here: the DUPLO is not double the size of the LEGO, it’s octuple the size. The ruler, conveniently, is useless in regards measuring volume. So, we’ve violated our initial maxim of doubling ‘everything.’
Here’s where we’d run into trouble. If we are to double everything, then that means doubling the length, height, width, and volume, which is impossible.
Doubling the size of the Earth (and everything on it) would lead to an 8x magnification of volume, and us being 16 times as heavy (if I calculated it correctly). Then there’s the problem of doubling the gravitational force…which would make us 32 times as heavy. This would likely be noticeable. However, the example is moot anyway because if the Earth is 8x the volume it was, then *everything* didn’t double. I can’t see a way around this.
I don’t understand — rulers are great tools for measuring volume. If the LEGO brick is one centimeter by one centimeter by one centimeter, the volume is one cubic centimeter. And you can measure it with a ruler. If the LEGO doubles in size to the size of a DUPLO LEGO brick and the ruler also doubles in size, the DUPLO LEGO will measure one centimeter by one centimeter by one centimeter — one cubic centimeter. One cubic centimeter is the volume.
You could dip your brick in a tub and measure the displacement, but I assure you, dipping the newly doubled brick in a now-doubled tub will yield the same results. You’ll use your new ruler to measure the length and width of the tub. Then you’ll use the ruler to measure the height change in the water and you will calculate one cubic centimeter of displacement.
You say, “Doubling the size of the Earth would lead to 8x magnification of volume.” What exactly would you be using to measure that volume that wouldn’t have been altered by the great doubling?
The exercise is kind of silly. One guy has to pretend to forget to double something so the other guy can say, “Ah, but I said double EVERYTHING!” Why not just skip to the end, if EVERYTHING doubled there would be nothing of the former size to compare it to and therefore no way of knowing that it doubled.
Things wouldn’t be heavier, gravity wouldn’t be weaker, volumes and masses wouldn’t change in disproportion to distances…
But there must be something I’m missing because you said, “…it’s impossible to know where to stop.” Everything means everything. Why stop? Is that the point? To see how far you would have to go before someone wouldn’t know there was a doubling, but someone else, an observer, would?
Regarding the ruler: I meant the ruler in the hypothetical photo would be useless for measuring volume. Since it’s just a picture, I can see that it is the same ruler as it was in the other picture, but I wouldn’t be able to pick it up and actually measure the DUPLO. But I see what you mean, you could see the picture of the ruler, and kind of determine that one centimeter on that ruler is roughly the length of one side of the DUPLO.
My friend and I would get caught up in this, too. One time, we broke the question down into two parts:
1) Did everything double?
2) Can you tell?
In the case of the LEGO-to-DUPLO, I see your argument that a person would be unable to tell (so thus part #2 is satisfied). However, everything did not double – in order to trick the observer (to satisfy #2), we had to octuple the volume of the cube, even though our observer was successfully duped.
The question is, probably, too crude. My friend would ask, “If everything was double, would we notice?” I would argue that it would be immediately noticeable – for example, doubling my height and weight would lead me to being over 11 feet tall, but weighing *only* about 320 pounds. (My son, meanwhile, would be well over 6 feet tall, but wouldn’t even weight 100 pounds.)
“Ah,” my friend would say, “but if pounds and inches themselves were doubled…”
“Still,” I would say, “I would feel something was not ‘right.'” Just because we’ve switched rod sticks, doesn’t mean I can’t feel it.
When I said “it’s impossible to know where to stop,” I was meaning this: my friend would generally start by just concerning himself with the physical sizes: such as height and volume. But what about forces? Would we have to double gravity? Gravity doesn’t really have a ‘size’ to double. Even if we agree to double the force of gravity, too, we’d still notice because distances would also have doubled, and gravity’s force would have dropped off as per the inverse square law, and doubling its force wouldn’t compensate correctly. And what about things such as back accounts and populations…doubling those would be immediately apparent.
Since it’s too crazy, maybe a better question would be, If X changed in force/size, how would we notice, or how would it affect our world?